the inaugural balls

about
The structures I eventually built are quite straightforward - two enantiomers (left- and right-handed versions) of a snub dodecahedron, like the two computer-generated figures on the right.
These shapes have been known for thousands of years. But the path to that choice was not so straightforward, so I describe it below.

problem
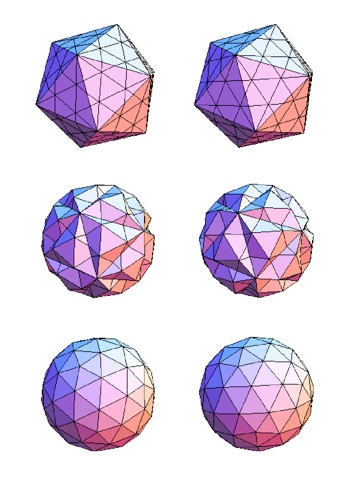
The two icosahedra in the first row at left correspond to the paper models above. The intersections of the lines on the surface of the icosahedron correspond to the new vertices of a chiral geodesated structure.
In this particular case, there are seven (T=7) small triangles for every one original triangle. (The Assembly Of Geod has T=9 and is not chiral). The original triangles are equilateral of course, because they are the faces of a regular icosahedron. The faces of the derived structure will not in general be equilateral.
The second pair on the left shows the new vertices “blown up” (actually pushed out radially) to be on the surface of a single circumscribing sphere.
The third row shows what happens when the original edges of the icosahedron are removed, because none of the new edges of the new structure follow the original edges.
Great! Or, maybe not... Because I think if I built these two, even at large scale, no-one would be able to tell the difference between them. In fact, most people would probably think they were the same as what I had already built!
So there we were. Nice models, but I had lost enthusiasm, and my project stalled. For months.
solution
Fortunately, in an exchange of email, Jim Hausman looked at the Tubespace model above and said something like “that’s just the snub dodecahedron with pentagonal caps, isn’t it?” And it is, more or less. So I built Tubespace models of enantiomeric snub dodecahedra (you see me holding them in one or two of the photos to help figure out which big structure corresponds to which model), and found three advantages:
1) all the edges are the same length (whereas the T=7 geodesic sphere has four sets of edges with different lengths)
2) the pentagonal holes make the left-and right-handedness a bit more visible (although you be the judge of that)
3) and then I thought – a tree trunk would fit perfectly through those pentagons! They might look pretty cool
around a couple of trees, they would be off the ground, and harder to steal (and that’s another TAOG story…)
Five advantages! And so it went.
And now I do plan to build one large chiral T=7 geodesic sphere (not the pair), at a secret location in Arizona in 2010 :-)
chiral
I’ve always been interested in chirality - handedness, a type of asymmetry - first in chemistry, then in biological molecules, including viruses. I was fascinated to discover, first from Joe Clinton’s work, then from George Hart’s, that a class of triangulated geodesic domes was chiral.
So after The Assembly Of Geod, I thought of building two enantiomeric (mirror-image) geodesic spheres based on the icosahedron, like the Tubespace model to the right. Since then, George Hart has constructed chiral geodesic structures of greater frequency, and complexity.
The lines on the icosahedral paper models to the right, and below, show where the edges would be on left- and right-handed geodesic spheres, if you blew them up to be more nearly spherical. So the next thing to do was to “blow them up” in the computer.